From Wikipedia, the free encyclopedia
The Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. This is the passive transformation point of view. The equations below, although apparently obvious, break down at speeds that approach the speed of light due to physics described by Einstein's theory of relativity.
Galileo formulated these concepts in his description of uniform motion [1] The topic was motivated by Galileo's description of the motion of a ball rolling down a ramp, by which he measured the numerical value for the acceleration of gravity, at the surface of the Earth. The descriptions below are another mathematical notation for this concept.
Contents[hide] |
[edit] Translation
In essence, the Galilean transformations embody the intuitive notion of addition and subtraction of velocities. The assumption that time can be treated as absolute is at the heart of the Galilean transformations.
This assumption is abandoned in the Lorentz transformations. These relativistic transformations are deemed applicable to all velocities, whilst the Galilean transformation can be regarded as a low-velocity approximation to the Lorentz transformation.
The notation below describes the relationship under the Galilean transformation between the coordinates (x,y,z,t) and (x′,y′,z′,t′) of a single arbitrary event, as measured in two coordinate systems S and S', in uniform relative motion (velocity v) in their common x and x’ directions, with their spatial origins coinciding at time t=t'=0: [2] [3] [4] [5]
Note that the last equation expresses the assumption of a universal time independent of the relative motion of different observers.
[edit] Galilean transformations
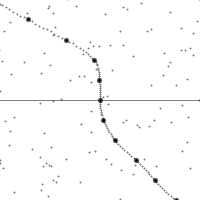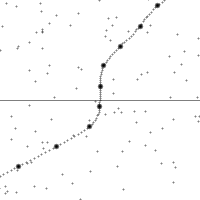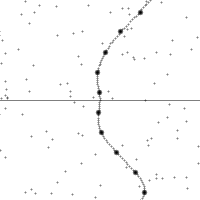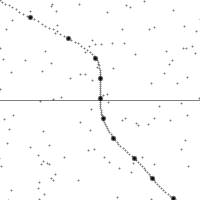
Vertical direction indicates time. Horizontal indicates distance, the dashed line is the spacetime trajectory of the observer. The lower half of the diagram shows events in the past. Upper half shows future events. The small dots are arbitrary events in spacetime.
The slope of the world line (deviation from being vertical) gives the relative velocity to the observer. Note how the view of spacetime shears when the observer accelerates.
Under the Erlangen program, the space-time (no longer spacetime) of nonrelativistic physics is described by the symmetry group generated by Galilean transformations, spatial and time translations and rotations.
The Galilean symmetries (interpreted as active transformations):
Spatial translations:
Time translations:
Rotations and Reflections:
where R is an orthogonal matrix.
[edit] Central extension of the Galilean group
The Galilean group: Here, we will only look at its Lie algebra. It's easy to extend the results to the Lie group. The Lie algebra of L is spanned by E, Pi, Ci and Lij (antisymmetric tensor) subject to commutators (operators of the form [,]), where
H is generator of time translations (Hamiltonian), Pi is generator of translations (momentum operator), Ci is generator of Galileian boosts and Lij stands for a generator of rotations (angular momentum operator).
We can now give it a central extension into the Lie algebra spanned by H', P'i, C'i, L'ij (antisymmetric tensor), M such that M commutes with everything (i.e. lies in the center, that's why it's called a central extension) and
[edit] Notes
- ^ Galileo 1638 Discorsi e Dimostrazioni Matematiche, intorno á due nuoue scienze 191 - 196, published by Lowys Elzevir (Louis Elsevier), Leiden, or Two New Sciences, English translation by Henry Crew and Alfonso de Salvio 1914, reprinted on pages 515-520 of On the Shoulders of Giants: The Great Works of Physics and Astronomy. Stephen Hawking, ed. 2002 ISBN 0-7624-1348-4
- ^ Mould, Richard A. (2002), Basic relativity, Springer-Verlag, ISBN 0-387-95210-1, http://books.google.be/books?id=lfGE-wyJYIUC&pg=PA42, Chapter 2 §2.6, p. 42
- ^ Lerner, Lawrence S. (1996), Physics for Scientists and Engineers, Volume 2, Jones and Bertlett Publishers, Inc, ISBN 0-7637-0460-1, http://books.google.be/books?id=B8K_ym9rS6UC&pg=PA1047, Chapter 38 §38.2, p. 1046,1047
- ^ Serway, Raymond A.; Jewett, John W. (2006), Principles of Physics: A Calculus-based Text, Fourth Edition, Brooks/Cole - Thomson Learning, ISBN 0-534-49143-X, http://books.google.be/books?id=1DZz341Pp50C&pg=PA261, Chapter 9 §9.1, p. 261
- ^ Hoffmann, Banesh (1983), Relativity and Its Roots, Scientific American Books, ISBN 0-486-40676-8, http://books.google.be/books?id=JokgnS1JtmMC&pg=PA83, Chapter 5, p. 83

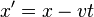
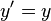



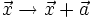


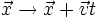

![[H,P_i]=0 \,\!](http://upload.wikimedia.org/math/3/b/9/3b9ee15117505a3832f6967d29293a3c.png)
![[P_i,P_j]=0 \,\!](http://upload.wikimedia.org/math/7/1/4/714ee7c4593f9d028979d594a444a160.png)
![[L_{ij},H]=0 \,\!](http://upload.wikimedia.org/math/b/7/9/b79c8bd2f74440e460c86eb5377fc578.png)
![[C_i,C_j]=0 \,\!](http://upload.wikimedia.org/math/9/6/b/96bbec83e55ace393e4a1ae676f802ea.png)
![[L_{ij},L_{kl}]=i [\delta_{ik}L_{jl}-\delta_{il}L_{jk}-\delta_{jk}L_{il}+\delta_{jl}L_{ik}] \,\!](http://upload.wikimedia.org/math/6/d/1/6d195435072f3a0ee98ee87c3b02e634.png)
![[L_{ij},P_k]=i[\delta_{ik}P_j-\delta_{jk}P_i] \,\!](http://upload.wikimedia.org/math/8/6/e/86eb87395a5586bf2b63f10150abeea6.png)
![[L_{ij},C_k]=i[\delta_{ik}C_j-\delta_{jk}C_i] \,\!](http://upload.wikimedia.org/math/4/4/4/444f85a225c2423c5557a0192b487d5c.png)
![[C_i,H]=i P_i \,\!](http://upload.wikimedia.org/math/d/e/3/de3d3052ab840b890f1a56224ae369d1.png)
![[C_i,P_j]=0 \,\!.](http://upload.wikimedia.org/math/3/4/e/34e01f1d9dd41a2c9ec63390fcabdc4d.png)
![[H',P'_i]=0 \,\!](http://upload.wikimedia.org/math/0/d/9/0d9049dc03e049c8161a4e26e05099ea.png)
![[P'_i,P'_j]=0 \,\!](http://upload.wikimedia.org/math/e/4/1/e416d2fe973d9378e11cba0a9b9a705d.png)
![[L'_{ij},H']=0 \,\!](http://upload.wikimedia.org/math/f/1/8/f188a60185ab7fdb0c3d80f5dd6661a7.png)
![[C'_i,C'_j]=0 \,\!](http://upload.wikimedia.org/math/e/5/b/e5b3a1020639092d849c1d517fb52ccf.png)
![[L'_{ij},L'_{kl}]=i [\delta_{ik}L'_{jl}-\delta_{il}L'_{jk}-\delta_{jk}L'_{il}+\delta_{jl}L'_{ik}] \,\!](http://upload.wikimedia.org/math/c/9/f/c9ff7a523ac9ddf92e189759ffb511d6.png)
![[L'_{ij},P'_k]=i[\delta_{ik}P'_j-\delta_{jk}P'_i] \,\!](http://upload.wikimedia.org/math/d/9/c/d9c5e3d0fc204f52638bd55aed7d7113.png)
![[L'_{ij},C'_k]=i[\delta_{ik}C'_j-\delta_{jk}C'_i] \,\!](http://upload.wikimedia.org/math/9/1/8/918cad3fd07f53ab6d5911024629b97f.png)
![[C'_i,H']=i P'_i \,\!](http://upload.wikimedia.org/math/d/0/3/d036b2bcad51e54202dfc7a23adc0733.png)
![[C'_i,P'_j]=i M\delta_{ij} \,\!](http://upload.wikimedia.org/math/7/5/2/752bce942b5df09eb0364dd487d7f380.png)
Tidak ada komentar:
Posting Komentar